Et voilà, l'heure véridique est arrivée! Examen de statistique demain!
Hmmm... on a droit à un formulaire... et ça, ça me dépasse. Parce que on n'a pas tellement besoin d'apprendre de formules par coeur, sincèrement... tout découle de soi... mais bon...
J'ai ben hâte de voir. J'espère qu'il n'y aura pas de questions chiennes genre "montrez que tel estimateur très laid est sans biais", tandis qu'on a genre vu ça une fois pi que c'est tellement tough, ou encore "montrez que telle affaire suit une distribution de Fisher"... on n'a genre... même pas vu ça.
Autrement, je devrais survivre! Checkez-le ben poser une question chienne! Je l'attends, il va se la jouer lopette!
m'haha... en plus je vais utiliser ma calculatrice pour trouver la moyenne pi l'écart-type échantillonnal, et ce même si j'ai peut-être pas le droit! Haha allô l'économie de temps!
Bon, ça n'intéresse personne de toute façon... souhaitez-moi bonne chance!
Pour les intéressés, regardez l'image suivante:
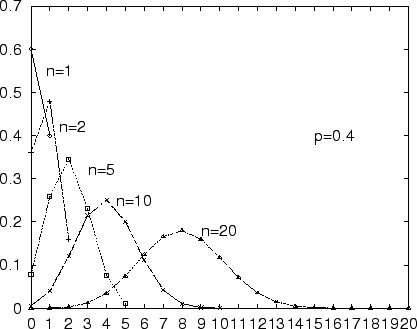
Ce qui est merveilleux avec ça, c'est que tout ce qu'on veut c'est que les variables aléatoires soient iid (indépendantes et identiquement distribuées), peu importe la distribution de chacune des variables. C'est pas merveilleux? C'est fort comme théorème...
Pour le dire dans le langage de tous les jours: on peut prédire assez bien un certain phénomène, à condition qu'on ait assez de données sur plusieurs réalisations dudit phénomène, et que toutes les réalisations soient indépendantes. On peut ne rien connaître sur le phénomène, c'est-à-dire être incapable de prédire le résultat de telle ou telle expérience, mais on sait à peu près ce que plusieurs événements donneront en moyenne.
Bon, j'ai fini de m'émerveiller... :)
Hmmm... on a droit à un formulaire... et ça, ça me dépasse. Parce que on n'a pas tellement besoin d'apprendre de formules par coeur, sincèrement... tout découle de soi... mais bon...
J'ai ben hâte de voir. J'espère qu'il n'y aura pas de questions chiennes genre "montrez que tel estimateur très laid est sans biais", tandis qu'on a genre vu ça une fois pi que c'est tellement tough, ou encore "montrez que telle affaire suit une distribution de Fisher"... on n'a genre... même pas vu ça.
Autrement, je devrais survivre! Checkez-le ben poser une question chienne! Je l'attends, il va se la jouer lopette!
m'haha... en plus je vais utiliser ma calculatrice pour trouver la moyenne pi l'écart-type échantillonnal, et ce même si j'ai peut-être pas le droit! Haha allô l'économie de temps!
Bon, ça n'intéresse personne de toute façon... souhaitez-moi bonne chance!
Pour les intéressés, regardez l'image suivante:

Ce qui est merveilleux avec ça, c'est que tout ce qu'on veut c'est que les variables aléatoires soient iid (indépendantes et identiquement distribuées), peu importe la distribution de chacune des variables. C'est pas merveilleux? C'est fort comme théorème...
Pour le dire dans le langage de tous les jours: on peut prédire assez bien un certain phénomène, à condition qu'on ait assez de données sur plusieurs réalisations dudit phénomène, et que toutes les réalisations soient indépendantes. On peut ne rien connaître sur le phénomène, c'est-à-dire être incapable de prédire le résultat de telle ou telle expérience, mais on sait à peu près ce que plusieurs événements donneront en moyenne.
Bon, j'ai fini de m'émerveiller... :)

5 commentaires:
"Pour le dire dans le langage de tous les jours: on peut prédire assez bien un certain phénomène, à condition qu'on ait assez de données sur plusieurs réalisations dudit phénomène,"
Donc si on mange trop nos fesses vont ressembler a une courbe de tendance naturelle
-jul
c'était en fait pas mal la conclusion à laquelle j'étais arrivée aussi, Julien.. à moins que j'interprète mal ce que tu dis.. mais je ne pense pas, ton analyse a l'air correcte
ben en fait... ce qu'on pourrait faire, cest prendre genre 20 personnes, leur faire manger plein de cochonneries, et regarder en moyenne de combien de cm leurs fesses ont grossie... et là soit cest une loi normale, soit on espère que 20 personnes ce sera suffisant (lol), et on calcule par exemple un intervalle de confiance à un certain pourcentage sur la "vraie" moyenne, c'est-à-dire si toute la planète suivait l'expérience... on peut faire pareil avec la variance, mais là cest pas une loi normale, c une loi du Chi-deux :)
le Chi-deux!!! j'en ai fais bcp des test the chi-carré dans mon projet de physique au cegep :) ON avait environ 240x30x30 valeurs(c'etait un chi-deux sur une surface)
-jul
tu t'en servais sûrement pour tester l'indépendance entre les variables?
moi j'ai juste fait ça au cégep, pas à luqàm... jai fait des test dhypothèses sur la variance avec le chi-carré, parce que (n-1)*s^2/sigma^2, où s^2 est la variance de l'échantillon et sigma^2 la variance (inconnue) de la population suit justement une distribution du chi-deux à (n-1) degrés de liberté.
je ne pense même pas quon va tester l'indépendant... jpense que là on va commencer la distribution de Fisher (quotient de deux variables aléatoires qui suivent une distribution du chi-deux, chacune divisées par leur degré de liberté respectif, anyway...). de toute manière, tout ce qu'on fait au cégep est inutile :(
what up yo chill out!
Publier un commentaire