dimanche 19 septembre 2010
ChessCube, Cubits & Fortune
Bonsoir chères gens.
Ce soir, je partage avec vous la Vérité. Cette Vérité vous permettra de devenir riche en utilisant l'incompréhension des gens. C'est permis et légal, et non seulement ça mais c'est impossible réussir si les gens floués ne sont pas consentants, i.e. si vous réussissez, c'est que quelqu'un a accepté de se faire flouer.
ChessCube
ChessCube est un site où l'on peut jouer aux échecs en temps réel.

C'est un site qui à la base était gratuit, mais qui a maintenant un système de monnaie permettant d'acheter des adhésions (qui elles donnent droit à certains avantages) et d'autres trucs comme visionner des vidéos de leçons. Cette monnaie, qui est le sujet de cet article, se nomme Cubits.
Cubits
Les Cubits, tel que susmentionné, sont utilisés pour se procurer des adhésions ou des privilèges quelconques sur ChessCube.

Comme le vrai argent, les Cubits peuvent (et doivent) être "pariés" sur les parties. En fait, c'est tout simple: pour chaque partie chaque joueur met en jeu une certaine quantité de Cubits (choix prédéfinis) et le vainqueur remporte une partie du pot, le restant étant perdu. (On remarquera que cela signifie effectivement que ChessCube "récupère" les Cubits achetés et garde simplement l'argent -- c'est un rake). Si aucun Cubits n'est misé, chaque joueur perd 3 Cubits à la fin de la partie (gagnant ou non).
Sinon, le vainqueur récupère sa mise initiale plus entre 90% et 97.5% de la mise de son adversaire. Par exemple, pour une partie où chaque joueur met 100 Cubits en jeu, le vainqueur pourrait gagner 90 Cubits et le perdant perdrait 100 Cubits.
So far so good?
Niveau de jeu & cote
Quantifier le talent de quelqu'un peut être fastidieux. Quantifier le talent de quelqu'un dans un référentiel comparatif à d'autres joueurs est plus simple. Avec un système de cote (typiquement le classement Elo) on peut classer les joueurs par force de jeu en assignant une valeur numérique à l'évaluation de leur jeu. Cette évaluation fluctue à mesure que les joueurs jouent, et la fluctuation dépend de plusieurs facteurs mais principalement de sa propre évaluation ainsi que l'évaluation de son adversaire.
Voici la formule utilisée sur ChessCube:
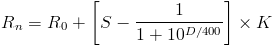
où R_n est la nouvelle cote du joueur, R_0 la cote initiale du joueur, S le résultat de la partie (1 pour une victoire, 1/2 pour une nulle, 0 pour une défaite), D la différence entre la cote de l'adversaire et la cote du joueur, et K un facteur d'amplification utilisé pour déterminer le nombre de points maximal qu'un joueur peut gagner (ou perdre) dans une partie.
Habituellement, la valeur de |D| est limitée à 400. Sur ChessCube, la formule ne limite pas le D, mais il est impossible de jouer contre quelqu'un coté plus ou moins que 500 de notre propre cote. De ce fait, la limite de |D| est à 500. De plus, le K varie en fonction du nombre de parties jouées dans une catégorie (bullet, blitz, standard) ainsi que par catégorie, contrairement aux endroits habituels (32 sur ICC, 15 à la FIDÉ, ...). M'enfin.
Le talent ne dépend pas de la cote
Depuis tantôt je dis que pour dire si quelqu'un est bon ou non on regarde sa cote. C'est vrai mais simplement parce que la cote est le meilleur indicateur de talent qui soit disponible "facilement". Par contre, la plupart des gens ne semblent pas réaliser que le talent ne dépend pas de la cote; c'est en fait le contraire.
Cela dit, il arrive que nous ayons de mauvaises soirées ou whatever. La cote varie donc. Ce qu'il faut comprendre est que la cote fluctue alentour d'un indicateur "réel" qui représente le talent intrinsèque de chaque personne. Chaque personne a donc deux cotes (conceptuellement):
La formule indique implicitement la probabilité de victoire
Postulat: comme le talent ne dépend pas de la cote et que la cote est le meilleur indicateur de talent, pour deux joueurs dont la cote est actuellement à son niveau le plus réaliste, la formule de la cote devrait être telle qu'une infinité de parties jouées entre les deux joueurs ne devrait pas affecter les cotes.
De cette manière, on peut déterminer la probabilité implicite de victoire (ou de défaite) pour chacun des joueurs. Pour fins de simplicité, nous supposerons par la suite que les nulles n'existent pas (les nulles ont tendance à produire des résultats relativement stables de toute façon).
Ainsi, pour les paramètres donnés plus haut, il faut que la variation suite à une partie soit en moyenne de 0. Cela implique donc que
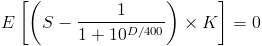
Après réarrangement et simplification:
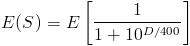
S peut prendre 3 valeurs: 1 avec probabilité p (victoire), 1/2 avec probabilité 0 (par hypothèse) et 0 avec probabilité q (défaite). E(S) vaut donc p qui est ce que l'on cherche.
Le deuxième terme se calcule très mal car l'espérance de 10^(D/400) est dégueulasse. La fonction est légèrement asymétrique vers la droite. Pour les fins de notre simulation, nous prendrons D = d = R_0(adversaire) - R_0. L'erreur se situe en dessous de 0.5%. Nous avons donc tout ce qu'il nous faut pour calculer une probabilité de victoire.
Le partage des Cubits est fait presque indépendamment des cotes
Comme je l'ai écrit plus haut, quand on gagne une partie, on gagne entre 90% et 97.5% de la mise initiale et on perd 100% de ce qui a été misé. Autrement dit, gagner contre quelqu'un de bien meilleur que moi ne m'apporte [presque] rien de plus que gagner contre quelqu'un de bien moins bon, la seule différence étant que je toucherai probablement 97.5% dans la première situation et 90% dans la deuxième situation.
THE MAGIC PLAN TO BECOME RICH!
Je suis coté environ 2100 sur ce site. En utilisant la formule trouvée plus haut, nous trouvons que la probabilité que je gagne une partie contre quelqu'un coté 1800 est d'environ 85% (sous les hypothèses actuelles, on a p = 1/(1+10^(-300/400)) = 0.849...).
Nous ferons l'hypothèse que je gagne 90% de la mise de Cubits si je suis mieux coté que la personne et que je gagne 97.5% de la mise si je suis moins bien coté. Cela signifie que je pourrais gagner 450 Cubits par partie (si je gagne) ou bien en perdre 500 si je perds. Pour arriver kif-kif au final, il faudrait que je gagne 52,6316% de mes parties, ce qui est bien inférieur au 85% implicite.
CONCLUSION: vous l'aurez deviné... à long terme, jouer contre ce paumé me rapportera beauuuuucoup de Cubits et ma cote ne changera pas (car ma cote ne représente que mon talent et mon talent est indépendant de ma cote).
La stratégie optimale est donc toute simple: jouer contre des joueurs bien moins bons que soi pour beaucoup de Cubits.
La beauté de la chose est que la plupart des gens préfèrent jouer contre des joueurs meilleurs que soi. Je n'ai même pas de difficulté à jouer contre des 1800, et tout le monde n'y voit que du feu.
Mais Philippe, il y a certainement un flaw quelque part dans ton raisonnement, ça ne peut pas être vrai.
Non les amis... ça marche. Je le sais parce qu'il n'y a pas si longtemps j'avais 3,000 Cubits. J'en ai maintenant 6,500. C'est assez pour m'acheter 1 mois d'adhésion (les tarifs étant 4,950 pour 1 mois, 9,950 pour 3 mois, 14,950 pour 1 an). À 1,000 Cubits par dollar, I am raking the big bucks.
Je me suis amusé à faire des simulations avec Excel avec les mêmes données que celles décrites ici (ma cote réelle = 2100, cote réelle de mon adversaire = 1800, K = 50, probabilité de victoire = 85%, solde initial = 3,000, mise par partie = 500).
Pour la simulation que je regarde actuellement:
Comme on s'y attendait, la cote ne bouge pratiquement pas (elle fluctue alentour du "talent réel"), et le solde augmente constamment en moyenne.
Ce soir, je partage avec vous la Vérité. Cette Vérité vous permettra de devenir riche en utilisant l'incompréhension des gens. C'est permis et légal, et non seulement ça mais c'est impossible réussir si les gens floués ne sont pas consentants, i.e. si vous réussissez, c'est que quelqu'un a accepté de se faire flouer.
ChessCube
ChessCube est un site où l'on peut jouer aux échecs en temps réel.

C'est un site qui à la base était gratuit, mais qui a maintenant un système de monnaie permettant d'acheter des adhésions (qui elles donnent droit à certains avantages) et d'autres trucs comme visionner des vidéos de leçons. Cette monnaie, qui est le sujet de cet article, se nomme Cubits.
Cubits
Les Cubits, tel que susmentionné, sont utilisés pour se procurer des adhésions ou des privilèges quelconques sur ChessCube.

Comme le vrai argent, les Cubits peuvent (et doivent) être "pariés" sur les parties. En fait, c'est tout simple: pour chaque partie chaque joueur met en jeu une certaine quantité de Cubits (choix prédéfinis) et le vainqueur remporte une partie du pot, le restant étant perdu. (On remarquera que cela signifie effectivement que ChessCube "récupère" les Cubits achetés et garde simplement l'argent -- c'est un rake). Si aucun Cubits n'est misé, chaque joueur perd 3 Cubits à la fin de la partie (gagnant ou non).
Sinon, le vainqueur récupère sa mise initiale plus entre 90% et 97.5% de la mise de son adversaire. Par exemple, pour une partie où chaque joueur met 100 Cubits en jeu, le vainqueur pourrait gagner 90 Cubits et le perdant perdrait 100 Cubits.
So far so good?
Niveau de jeu & cote
Quantifier le talent de quelqu'un peut être fastidieux. Quantifier le talent de quelqu'un dans un référentiel comparatif à d'autres joueurs est plus simple. Avec un système de cote (typiquement le classement Elo) on peut classer les joueurs par force de jeu en assignant une valeur numérique à l'évaluation de leur jeu. Cette évaluation fluctue à mesure que les joueurs jouent, et la fluctuation dépend de plusieurs facteurs mais principalement de sa propre évaluation ainsi que l'évaluation de son adversaire.
Voici la formule utilisée sur ChessCube:
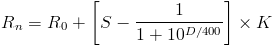
où R_n est la nouvelle cote du joueur, R_0 la cote initiale du joueur, S le résultat de la partie (1 pour une victoire, 1/2 pour une nulle, 0 pour une défaite), D la différence entre la cote de l'adversaire et la cote du joueur, et K un facteur d'amplification utilisé pour déterminer le nombre de points maximal qu'un joueur peut gagner (ou perdre) dans une partie.
Habituellement, la valeur de |D| est limitée à 400. Sur ChessCube, la formule ne limite pas le D, mais il est impossible de jouer contre quelqu'un coté plus ou moins que 500 de notre propre cote. De ce fait, la limite de |D| est à 500. De plus, le K varie en fonction du nombre de parties jouées dans une catégorie (bullet, blitz, standard) ainsi que par catégorie, contrairement aux endroits habituels (32 sur ICC, 15 à la FIDÉ, ...). M'enfin.
Le talent ne dépend pas de la cote
Depuis tantôt je dis que pour dire si quelqu'un est bon ou non on regarde sa cote. C'est vrai mais simplement parce que la cote est le meilleur indicateur de talent qui soit disponible "facilement". Par contre, la plupart des gens ne semblent pas réaliser que le talent ne dépend pas de la cote; c'est en fait le contraire.
Cela dit, il arrive que nous ayons de mauvaises soirées ou whatever. La cote varie donc. Ce qu'il faut comprendre est que la cote fluctue alentour d'un indicateur "réel" qui représente le talent intrinsèque de chaque personne. Chaque personne a donc deux cotes (conceptuellement):
- Sa cote actuelle
- Sa cote réelle représentant réellement son talent
La formule indique implicitement la probabilité de victoire
Postulat: comme le talent ne dépend pas de la cote et que la cote est le meilleur indicateur de talent, pour deux joueurs dont la cote est actuellement à son niveau le plus réaliste, la formule de la cote devrait être telle qu'une infinité de parties jouées entre les deux joueurs ne devrait pas affecter les cotes.
De cette manière, on peut déterminer la probabilité implicite de victoire (ou de défaite) pour chacun des joueurs. Pour fins de simplicité, nous supposerons par la suite que les nulles n'existent pas (les nulles ont tendance à produire des résultats relativement stables de toute façon).
Ainsi, pour les paramètres donnés plus haut, il faut que la variation suite à une partie soit en moyenne de 0. Cela implique donc que
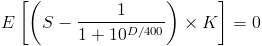
Après réarrangement et simplification:
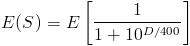
S peut prendre 3 valeurs: 1 avec probabilité p (victoire), 1/2 avec probabilité 0 (par hypothèse) et 0 avec probabilité q (défaite). E(S) vaut donc p qui est ce que l'on cherche.
Le deuxième terme se calcule très mal car l'espérance de 10^(D/400) est dégueulasse. La fonction est légèrement asymétrique vers la droite. Pour les fins de notre simulation, nous prendrons D = d = R_0(adversaire) - R_0. L'erreur se situe en dessous de 0.5%. Nous avons donc tout ce qu'il nous faut pour calculer une probabilité de victoire.
Le partage des Cubits est fait presque indépendamment des cotes
Comme je l'ai écrit plus haut, quand on gagne une partie, on gagne entre 90% et 97.5% de la mise initiale et on perd 100% de ce qui a été misé. Autrement dit, gagner contre quelqu'un de bien meilleur que moi ne m'apporte [presque] rien de plus que gagner contre quelqu'un de bien moins bon, la seule différence étant que je toucherai probablement 97.5% dans la première situation et 90% dans la deuxième situation.
THE MAGIC PLAN TO BECOME RICH!
Je suis coté environ 2100 sur ce site. En utilisant la formule trouvée plus haut, nous trouvons que la probabilité que je gagne une partie contre quelqu'un coté 1800 est d'environ 85% (sous les hypothèses actuelles, on a p = 1/(1+10^(-300/400)) = 0.849...).
Nous ferons l'hypothèse que je gagne 90% de la mise de Cubits si je suis mieux coté que la personne et que je gagne 97.5% de la mise si je suis moins bien coté. Cela signifie que je pourrais gagner 450 Cubits par partie (si je gagne) ou bien en perdre 500 si je perds. Pour arriver kif-kif au final, il faudrait que je gagne 52,6316% de mes parties, ce qui est bien inférieur au 85% implicite.
CONCLUSION: vous l'aurez deviné... à long terme, jouer contre ce paumé me rapportera beauuuuucoup de Cubits et ma cote ne changera pas (car ma cote ne représente que mon talent et mon talent est indépendant de ma cote).
La stratégie optimale est donc toute simple: jouer contre des joueurs bien moins bons que soi pour beaucoup de Cubits.
La beauté de la chose est que la plupart des gens préfèrent jouer contre des joueurs meilleurs que soi. Je n'ai même pas de difficulté à jouer contre des 1800, et tout le monde n'y voit que du feu.
Mais Philippe, il y a certainement un flaw quelque part dans ton raisonnement, ça ne peut pas être vrai.
Non les amis... ça marche. Je le sais parce qu'il n'y a pas si longtemps j'avais 3,000 Cubits. J'en ai maintenant 6,500. C'est assez pour m'acheter 1 mois d'adhésion (les tarifs étant 4,950 pour 1 mois, 9,950 pour 3 mois, 14,950 pour 1 an). À 1,000 Cubits par dollar, I am raking the big bucks.
Je me suis amusé à faire des simulations avec Excel avec les mêmes données que celles décrites ici (ma cote réelle = 2100, cote réelle de mon adversaire = 1800, K = 50, probabilité de victoire = 85%, solde initial = 3,000, mise par partie = 500).
Pour la simulation que je regarde actuellement:
- Solde après 5 parties: 4,300
- Cote après 5 parties: 2077
- Solde après 10 parties: 5,600
- Cote après 10 parties: 2075
- Solde après 20 parties: 9,150
- Cote après 20 parties: 2101
- Solde après 50 parties: 16,000
- Cote après 50 parties: 2051
- ...
- Solde après 5,000 parties: 1,516,940
- Cote après 5,000 parties: 2084
Comme on s'y attendait, la cote ne bouge pratiquement pas (elle fluctue alentour du "talent réel"), et le solde augmente constamment en moyenne.
vendredi 17 septembre 2010
vendredi 10 septembre 2010
jeudi 9 septembre 2010
jeudi 2 septembre 2010
S'abonner à :
Commentaires (Atom)
